2021ix9, Thursday: the truth behind the lie.

One of the great things about numbers is not that they can be used to lie, although they can.

It’s that even when they’re (mis-)used that way, sometimes the truth still lurks within.

I’m no great mathematician, although my daughter tells me that I light up when I’m working through problems with her to help her study. And it’s a sadness that when I studied maths in school, we focused on mechanics at the expense of statistics and probability.

I’ve picked up a bit of each since, although I’m still very rule-of-thumb. And every so often something comes up that simply delights me.

Benford’s Law was one such. I encountered it as a counter-fraud tool many years ago. For large number sets, it observes, the leading digit - that is, the lefthand-most one, denoting (say) the thousands in a four-digit number or the millions in a seven-digit one - is rarely an even distribution. No: a leading “1” is by far the commonest number, with a sharp drop to “2” and then a logarithmic curve flattening thereafter all the way to “9”.

Why is this useful in counter-fraud? Well, to make a fraud work, you often need to cook the books - to alter financial records. What are financial records but numbers? And when you make up numbers, or generate them randomly, you may well fail to make the statistical distribution of those numbers look right.

So if you’re looking at a data-set whose leading digits are evenly distributed - instead of, as Benford’s Law predicts, having as much as 30% of them start with a “1” - you ought to start getting suspicious.

I mention this having been pointed (by the ever-wonderful Charles Arthur) to a recent takedown of a seminal piece of counter-fraud research. The research, from 2012, posited that a measurable decrease in dishonesty could result from a simple change in how people sign declarations of honesty in documents. You know how at the bottom of a tax return, or form providing details for (say) insurance, you sign to say you've given accurate information? The research suggested that simply by putting the declaration at the top - that is, before you provide the information instead of afterwards - people would be significantly more likely to tell the truth.

Classic “nudge” theory at work, you might think.

Unfortunately, the authors themselves tried and failed to replicate their findings in 2020. They found anomalies in one of their key data sets, which they attributed to a “randomisation failure”.

No: as the new (and really smart and thoughtful) analysis says - conclusively, to my mind - the data in question was simply faked.

I won’t provide too much detail. The analysis is short, clear, and absolutely worth reading in full. To give just one example, it noted that the data (from a motor insurer) included two sets of mileage figures, both supposedly provided by drivers. But while the first set showed notable spikes in frequency for numbers ending either in “000” or “500” (that is: people roughly rounding their mileage to the nearest half-thousand, as you might well expect them to do), the second set was absolutely flat - as the graph reproduced below shows.

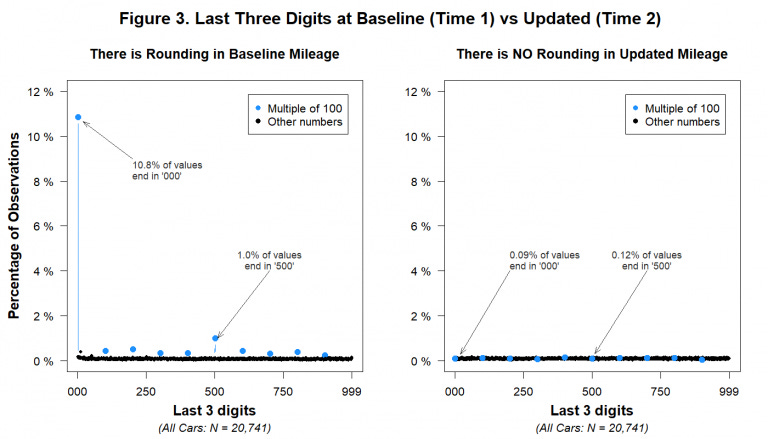
In other words: the same people were rough-guessing their mileage first time round, but giving it accurate to a single mile thereafter. Consistently. Everyone. Every time.

You’ve met humans. You tell me how plausible that sounds.

If anything, the analysis gets still more fascinating thereafter.

To their credit, all four of the 2012 authors recognise the problem, and have now retracted the 2012 paper. There’s no reason to think any of them were party to what now appears to have been an essentially made-up data set.

More importantly, they also agree with a core emergent finding of the writers of the new analysis. Research which doesn’t expose its underlying data (unless it’s absolutely impossible, say for personal privacy or safety purposes, to share it), isn’t to be trusted. Because it can’t be checked.

And given the reproducibility crisis, that just isn’t good enough.

I recognise that I seem to be straying a long way from the law, here - my usual stamping grounds.

But this is, to me, objectively interesting. There’s a beauty in the idea that those who lie with statistics may ultimately be found out by them too.

And there’s perhaps at least a small legal application - or at least a litigation one.

Numbers can be made to lie, sure. But equally, underneath the lying explanation there may be a true story begging to come out.

And - as we’ve discussed ad nauseam - advocacy is about story-telling. Don’t ignore the opportunity you have to use numbers to tell stories. If you can take a wall of impenetrable numbers, and - as the writers here have so lucidly done - use them to fashion a compelling, even shocking, narrative, which grabs the attention and answers the key questions, don’t waste it.

Not all of us advocates are numerate. Not all of us “get” statistics and probability. Some of us even misuse them - by accident or by design. But more of us should get it, and get it right. I know I’ve mentioned it before, but the Inns of Court College of Advocates guide, created with the help of the Royal Statistical Society, is a pretty good way to start.